Scale construction

Note to readers. More than the other pages, this page is a work in progress. I do not use scales much, and some issues that I raise on this page may be solved by work of which I am not yet aware! Things here could also be wrong. If you are a reader who knows about or works with scales, I’m always happy to hear your thoughts.

A case when scales work: A truly latent causal treatment

Suppose that $A_i \sim \mathcal{N}(0,1)$ is a latent variable that causes $Y_i$. We can’t see $A_i$ directly, but only indirect measures $X_{i1},X_{i2},X_{i3}$.

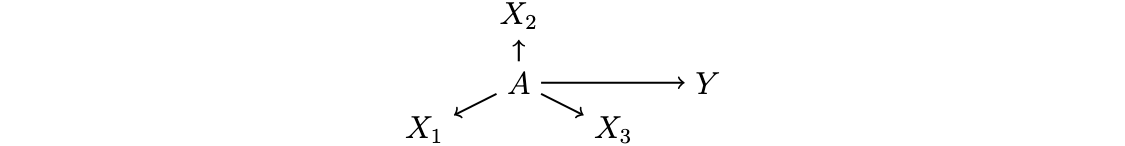
How should we estimate the causal effect of $A_i$ on $Y_i$? One way is by converting the measured variables into a scale. For example, we might define a measure $\tilde{A}_i$.

\[ \tilde{A}_i = \frac{1}{3}\left(X_{i1} + X_{i2} + X_{i3}\right) \]

This might be especially credible if the true data generating process were a linear model, such as each measure being a standard Normal draw centered on the true latent construct value $A_i$.

\[ X_{ij} \sim \mathcal{N}(A_i, 1) \]

In that case, one can show that our scale estimator has a known sampling distribution,

\[ \tilde{A}_i \sim \mathcal{N}(A_i, \sigma^2 = \frac{1}{3}) \]

under which the scale estimate equals the latent construct on average, but is estimated with some noise. The measure would be better if there were more $X$ variables providing many signals of the latent construct.

Suppose the true causal effect of $A$ on $Y$ followed a very simple linear functional form that could be well-summarized by coefficients $\alpha$ and $\beta$, which capture both a descriptive and a causal association because in this case $A\rightarrow Y$ is unconfounded.

\[ E(Y^a) = E(Y\mid A = a) = \alpha + \beta a \]

If one estimated by OLS regression of $Y$ on $\tilde{A}$, this would produce a downwardly biased estimator for $\beta$ because of measurement error in $\tilde{A}$. Because the measurement error in this simple model is by assumption known, one could correct for that error and produce an unbiased estimator for $\beta$ despite having not measured $A$ directly. First, we can derive the estimate when regressing $Y$ on $\tilde{A}$.

\[ \begin{aligned} \text{E}(Y\mid\tilde{A}) &= \tilde\alpha + \tilde\beta \tilde{A} \\ \hat{\tilde\beta} &= \frac{\text{Cov}(\tilde{A},Y)}{\text{Var}(\tilde{A})} \\ &= \frac{\text{E}\left(\text{Cov}(\tilde{A}, Y \mid A)\right) + \text{Cov}\left(\text{E}(\tilde{A}\mid A), \text{E}(Y\mid A)\right)}{\text{E}(\text{Var}(\tilde{A}\mid A)) + \text{Var}(\text{E}(\tilde{A}\mid A))} \\ &= \frac{ 0 + \text{Cov}(A, \alpha + \beta A) }{ \frac{1}{3} + \text{Var}(A) } \\ &= \frac{ \beta }{ \frac{1}{3} + 1 } \\ &= \frac{3}{4}\beta \end{aligned} \] Therefore one could arrive at the following strategy:

estimate $\tilde{A}$ by the average of $X_{i1}$, $X_{i2}, $X_{i3}$.
estimate $\hat{\tilde\beta}$ by regressing $Y$ on $\tilde{A}$
estimate $\hat\beta = \frac{4}{3}\hat{\tilde\beta}$

In the analysis above, a few things made this simple:

each measure $X_{ij}$ was linearly related to $A_i$
each measure had the same mean given $A_i$ and the same conditional variance
measures were independent given $A_i$: $X_{ij}\unicode{x2AEB} X_{ij'}\mid A_i$ for all $j$ and $j'$

Methods for factor analysis and scale construction can relax the criteria above. These are statistical issues that are solveable. A bigger reason to be skeptical about scales is as follows: what if the latent construct is not the causal force after all?

How scales can be problematic

Suppose the causal process is more accurately represented by the DAG below: each of the $X$ variables is a cause of $Y$, rather than the latent construct. There is actually no latent construct $A$ in the world; the variable $A$ is only a statistical tool that is a deterministic aggregation of the $X$ variables. Thus $A$ actually doe snot appear in the DAG at all! What has the causal power are the $X$ variables.

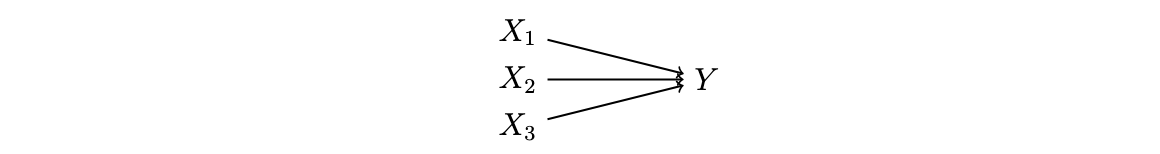
This may often be the setting in which social scientists use scales. A few examples:

Neighborhood disadvantage
- $A$ is neighborhood disadvantage
- $X$ variables are neighborhood-level poverty, crime, and presence of local nonprofits
- $Y$ is children’s high school completion rates
Academic achievement
- $A$ is academic achievement measured by GPA
- $X$ variables are grades in math, English, science, and social studies
- $Y$ is college enrollment
Voting patterns in Congress
- $A$ is a partisanship score (liberal to conservative)
- $X$ variables are voting patterns on fiscal, social, and foreign policy issues
- $Y$ is being re-elected

In each case, it is possible that each $X$ affects $Y$, rather than $A$ affecting $Y$. If we had enough data, it would be better to study the causal effect of each $X$ on $Y$ instead of aggregating them to a score.

Consistency goes wrong when you aggregate

What is the potential high school completion outcome $Y^a$ for a child assigned to grow up in a neighborhood assigned to disadvantaged score $a$? If poverty and crime each affect high school completion, then it would matter how you assign that child to this score: the outcome might depend on what mix of crime and poverty together create the score $a$.

Mathematically, the consistency assumption is no longer so clear. The potential outcome if assigned to treatment value $a$ is not fully defined. It might be better to study the potential outcome $Y^{x_1,x_2,x_3}$ to be realized if assigned to a neighborhood characterized by the specific set of treatment conditions $x_1$, $x_2$, and $x_3$.

A scale may still be useful in practice: there may be too few cases to yield a precise estimate of the joint causal effects of $X_1$, $X_2$, and $X_3$. It is possible that an estimator using the scale $Y^{\tilde{a}(x_1,x_2,x_3)}$ would actually be closer to $Y^{x_1,x_2,x_3}$ than an estimator that studies the full joint causal effects. This may be an open question.

What is relevant is that when using a scale, one ought to be transparent about the assumed model of the world and why the scale is useful.

Pros and cons

To recap, scales come with some pros and cons:

Pros
- simpler to study one scale than many causal inputs
- fewer causal estimates to report
- possible gains in statistical precision
Cons
- loss of concreteness: you can ask a policymaker to reduce poverty, but it is hard to ask a policymaker to intervene to change a latent scale
- a scale requires a model of how signals relate to the latent construct, and that model may be wrong
- a scale may create challenges for the consistency assumption

If using a scale, some things you want are:

as many signals of the latent construct as possible
independence of your signals
strong association between the latent construct and each signal

Much of the literature on scales focuses on these things because they are statistically tractable. But before using a scale, you should ask yourself whether a move from many concrete variables to one latent variable will improve or complicate your analysis.